
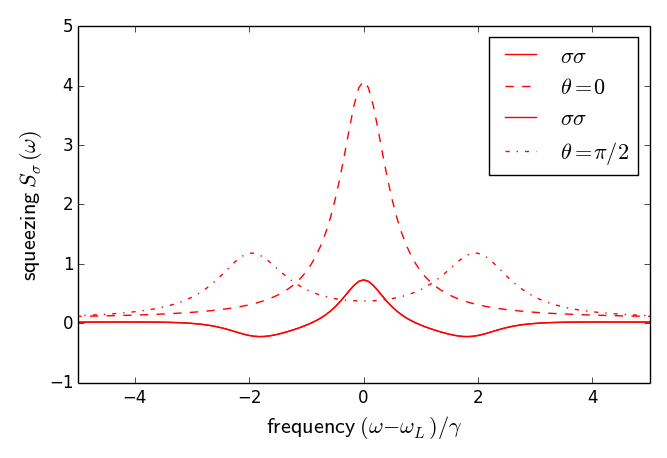
Squeezing correlations (left) and spectra (right) for a two-level atom. Parameters as in the script.
#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
Resonance fluorescence with the regression formula (SS 2017, QO II).
We have a routine that solves the Bloch equations with initial data
pe, pg, sigma (dipole). If one applies the regression hypothesis, we
need an initial state \sigma \rho whose expectation values are
Tr[ \pi_e \sigma \rho ] = 0, since \sigma = |g>,
Tr[ \sigma \sigma \rho ] = 0,
Tr[ \sigma^\dag \sigma \rho ] = <\pi_e>
* Note that complex conjugation does not hold any longer!
* This means that we have to re-write the equations in such a way
that conjugation is not 'hard-wired'.
"""
from pylab import *
from scipy.integrate import odeint
xsize = 6.5
ysize = 1.1*xsize*0.5*(sqrt(5.) - 1.)
mysize = 16
def setParameters(theta0 = 1.0*pi, phi0 = 0.):
# theta0 = pi (0) is ground (excited) state
"""
set parameters for two-level dynamics (Bloch equations)
cw = True: cw laser
cw = False: pulsed laser (length pulse_tau)
c0 = initial condition for two-level vector (pure state)
t = vector of times 0 < t < tMax where solution is plotted
(default) initial conditions with optional parameters theta0, phi0
"""
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e, cw, pulse_tau, c0, t, N_t, dt, \
Omega, Rabi_env
gamma_e = 1.
Gamma_eg = (0.0 + 0.5)*gamma_e # minimum value is 0.5*gamma_e
Atom_f = 200.*gamma_e
Laser_f = Atom_f + 0.0*gamma_e
Rabi_f = 2.0*gamma_e*exp(+0.0*pi*1j)
cw = True # False = pulsed laser
# pulse area is Rabi_f * sqrt(2*pi) * pulse_tau
pulse_tau = pi/abs(Rabi_f)/sqrt(2*pi)
# pulse_tau = 0.075/gamma_e
# pulse_tau = 1./gamma_e
if cw:
def Omega(t):
return 2.*real(Rabi_f*exp(-1j*Laser_f*t))
def Rabi_env(t):
return Rabi_f*ones_like(t)
else:
def Omega(t):
return 2.*real(Rabi_f*exp(-1j*Laser_f*t))*exp(-0.5*((t - pulse_tau)/pulse_tau)**2)
def Rabi_env(t):
return Rabi_f*exp(-0.5*((t - pulse_tau)/pulse_tau)**2)
# initial conditions, parametrized by angle theta0 on Bloch sphere,
# theta0 = 0 is excited state ('spin up')
# phi0 is relative phase, fixes phase of initial dipole
#
cg0, ce0 = sin(0.5*theta0)*exp(-1j*0.5*phi0), cos(0.5*theta0)*exp(1j*0.5*phi0)
c0 = (cg0, ce0)
# important to signal that c0 has complex entries, otherwise
# the conversion to real pairs does not work
c0 = array(c0, dtype=complex)
# interesting time interval
tMax = 3./gamma_e
tMax = 24.*max(3./gamma_e, 3.*pi/(gamma_e + abs(Rabi_f)))
N_t = 1024
t, dt = linspace(-0.0*pulse_tau, tMax, N_t, retstep = True)
return
def steady_state(trace_0 = 1.):
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e
Delta_L = Laser_f - Atom_f
denom = 0.5*gamma_e + 0.5*abs(Rabi_f)**2*Gamma_eg/(Gamma_eg**2 + Delta_L**2)
inversion = -0.5*gamma_e / denom
dipole = 0.5j*Rabi_f*inversion/(Gamma_eg - 1j*Delta_L)
pe = 0.5*(trace_0 + inversion)
pg = 0.5*(trace_0 - inversion)
return [pg, pe, dipole]
def BlochL_rwa(state, t):
"""
Bloch equations ('superoperator or Liouvillian L')
worked out for complex observables with the RWA
'state' = [pg, pe, sigma], this is *not* the Bloch vector!
"""
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e
(pg, pe, sigma) = state
dotsigma = -1j*(Atom_f - Laser_f)*sigma - Gamma_eg*sigma + \
0.5*1j*Rabi_env(t)*(pe - pg)
dotpe = - gamma_e*pe - imag(conj(Rabi_env(t))*sigma)
dotpg = - dotpe
return [dotpg, dotpe, dotsigma]
def r_BlochL_rwa(x, t, *args):
# mapping of BlochL to function of real parameters
state = x.view(complex128)
dstatedt = BlochL_rwa(state, t, *args)
return asarray(dstatedt, dtype=complex128).view(float64)
def xBlochL_rwa(xstate, t):
"""
extended Bloch equations ('superoperator or Liouvillian L')
not assuming that = conj()
'xstate' = [pg, pe, sigma, sigmaDag]
"""
global Rabi_f, Laser_f, Atom_f, Gamma_eg, gamma_e
(pg, pe, sigma, sigmaDag) = xstate
dotsigma = -1j*(Atom_f - Laser_f)*sigma - Gamma_eg*sigma + \
0.5*1j*Rabi_env(t)*(pe - pg)
dotsigmaDag = 1j*(Atom_f - Laser_f)*sigmaDag - Gamma_eg*sigmaDag - \
0.5*1j*conj(Rabi_env(t))*(pe - pg)
dotpe = - gamma_e*pe + 0.5j*(conj(Rabi_env(t))*sigma - Rabi_env(t)*sigmaDag)
dotpg = - dotpe
return [dotpg, dotpe, dotsigma, dotsigmaDag]
def r_xBlochL_rwa(x, t, *args):
# mapping of xBlochL to function of real parameters
state = x.view(complex128)
dstatedt = xBlochL_rwa(state, t, *args)
return asarray(dstatedt, dtype=complex128).view(float64)
if False:
# solve equations of motion, compare two versions of Bloch equations
#
setParameters()
print('solve two-level equations')
# solve with dissipation the Bloch equations, using the
# same initial state
(cg0, ce0) = c0
state0 = [abs(cg0)**2, abs(ce0)**2, conj(cg0)*ce0]
# 'extended state', with complex conjugate (sigmaDag) separately
xstate0 = [abs(cg0)**2, abs(ce0)**2, conj(cg0)*ce0, cg0*conj(ce0)]
#
# again, need to specify that these are tuples of complex numbers
state0 = array(state0, dtype=complex)
xstate0 = array(xstate0, dtype=complex)
# solve the Bloch equations (RWA version only)
#
rwa = odeint(r_BlochL_rwa, state0.view(float64), t, full_output = 1)
rwa = rwa[0].view(complex128)
#
bg_rwa = real(rwa[:,0])
be_rwa = real(rwa[:,1])
sigma_rwa = rwa[:,2]
xrwa = odeint(r_xBlochL_rwa, xstate0.view(float64), t, full_output = 1)
xrwa = xrwa[0].view(complex128)
#
bg_xrwa = real(xrwa[:,0])
be_xrwa = real(xrwa[:,1])
sigma_xrwa = xrwa[:,2]
sigmaDag_xrwa = xrwa[:,3]
# analytical solution for steady state
#
[pg, pe, dipole] = steady_state()
if True:
#
setParameters()
print('solve two-level correlations')
# analytical solution for steady state
#
[pg, pe, dipole] = steady_state()
# solve Bloch equations in the regression sense, take
# modified initial state from sigma rho_ss and from sigma rho_ss sigmaDag
# (intensity correlations)
#
xstate_ss = [dipole, 0., 0., pe]
xstate_ss = array(xstate_ss, dtype=complex)
# solve the RWA version of Bloch equations
#
corr = odeint(r_xBlochL_rwa, xstate_ss.view(float64), t, full_output = 1)
corr = corr[0].view(complex128)
#
bg_corr = real(corr[:,0])
be_corr = real(corr[:,1])
sigma_corr = corr[:,2]
sigmaDag_corr = corr[:,3]
# for intensity correlations
xstate_ss = [pe, 0., 0., 0.] # should be the ground state
xstate_ss = array(xstate_ss, dtype=complex)
g2 = odeint(r_xBlochL_rwa, xstate_ss.view(float64), t, full_output = 1)
g2 = g2[0].view(complex128)
#
bg_g2 = real(g2[:,0])
be_g2 = real(g2[:,1]) # this is the G2(tau) correlation function
sigma_g2 = g2[:,2]
sigmaDag_g2 = g2[:,3]
# for squeezing correlations, quadrature phase
theta = 0.5*pi
xstate_ss = [exp(1j*theta)*dipole, exp(-1j*theta)*conj(dipole), \
exp(-1j*theta)*pg, exp(1j*theta)*pe]
xstate_ss = array(xstate_ss, dtype=complex)
sq_corr = odeint(r_xBlochL_rwa, xstate_ss.view(float64), t, full_output = 1)
sq_corr = sq_corr[0].view(complex128)
#
sq_sigma = sq_corr[:,2]
sq_sigmaDag = sq_corr[:,3]
sq_theta = exp(1j*theta)*sq_sigma + exp(-1j*theta)*sq_sigmaDag
if False:
# extract final (stationary?) state, can be compared to
# analytical results
#
g_ss = bg_rwa[-1]
e_ss = be_rwa[-1]
sigma_ss = sigma_rwa[-1]
g_xss = bg_xrwa[-1]
e_xss = be_xrwa[-1]
sigma_xss = sigma_xrwa[-1]
sigmaDag_xss = sigmaDag_xrwa[-1]
print('stationary state (standard / complexified)')
print('at time %3.4g / gamma_e' %(gamma_e*t[-1]))
print('p_e = %3.4g (%3.4g)' %(e_ss, e_xss))
print('p_g = %3.4g (%3.4g)' %(g_ss, g_xss))
print('p_e + p_g = %3.4g (%3.4g)' %(e_ss + g_ss, e_xss + g_xss))
print('sigma = %3.4g + %3.4g i (%3.4g + %3.4g i, %3.4g + %3.4g i)'
%(real(sigma_ss), imag(sigma_ss), real(sigma_xss), imag(sigma_xss),
real(sigmaDag_xss), -imag(sigmaDag_xss)))
print('theory:')
print('p_e = %3.4g' %(pe))
print('p_g = %3.4g' %(pg))
print('sigma = %3.4g + %3.4g i' %(real(dipole), imag(dipole)))
if False:
figure(2, (xsize, ysize), tight_layout = True)
plot( t, bg_rwa, 'b', lw = 1.5, label = 'g' )
plot( t, be_rwa, 'r', lw = 1.5, label = 'e' )
plot( t, real(sigma_rwa), 'g', lw = 1.5, label = '$\mathsf{Re\ }d$' )
plot( t, imag(sigma_rwa), 'g--', lw = 1.5, label = '$\mathsf{Im\ }d$' )
if False:
figure(2, (xsize, ysize), tight_layout = True)
plot( t, bg_xrwa, 'b+', label = 'g' )
plot( t, be_xrwa, 'r+', label = 'e' )
plot( t, real(sigma_xrwa), 'g+', label = '$\mathsf{Re\ }d$' )
plot( t, imag(sigma_xrwa), 'g+', label = '$\mathsf{Im\ }d$' )
plot( t, real(sigmaDag_xrwa), '.' )
plot( t, -imag(sigmaDag_xrwa), '.' )
ylim(-1, 1)
legend()
if False:
"""
compute spectrum of dipole correlation function,
should return Mollow triplet
"""
ddcorr = sigmaDag_corr - sigmaDag_corr[-1]
print('check stationary value of C_sigma: %3.4g + %3.4g i vs %3.4g'
%(real(sigmaDag_corr[-1]), imag(sigmaDag_corr[-1]), abs(dipole)**2) )
spec = 2*real(dt*fft(ddcorr))
figure(4, (xsize, ysize), tight_layout = True)
plot( t, real(sigmaDag_corr), 'b' )
plot( t, imag(sigmaDag_corr), 'r' )
t_max = 12./gamma_e
xlim(0, t_max)
plot( [0, t_max], [abs(dipole)**2, abs(dipole)**2], ':' )
spec = fftshift(spec)
omega = fftshift(2*pi*fftfreq(N_t, d = dt))
figure('Mollow', (xsize, ysize), tight_layout = True)
plot(omega/gamma_e, spec, 'r-')
om_max = max(2.5*sqrt(abs(Rabi_f)**2 + (Laser_f - Atom_f)**2), 3.*gamma_e)
xlim(-om_max, om_max)
xlabel(r'$\mathsf{frequency\ } (\omega - \omega_L)/\gamma$', size = mysize)
ylabel(r'$\mathsf{spectrum\ } S_d( \omega )$', size = mysize)
if True:
"""
compute 'squeezing spectrum' of correlation Q_sigma(t) =
"""
sqcorr = sigma_corr
print('check stationary value of Q_sigma: %3.4g + %3.4g i vs %3.4g + %5.4g i'
%(real(sqcorr[-1]), imag(sqcorr[-1]), \
real(dipole**2), imag(dipole**2)) )
# make plot of correlation function
figure(4, (xsize, ysize), tight_layout = True)
plot( t, real(sqcorr), 'b', label = 'Re Q' )
plot( t, imag(sqcorr), 'r', label = 'Im Q' )
# repeat for sigma_theta correlation function
sTheta_corr = sq_theta
dipole_theta = exp(1j*theta)*dipole + exp(-1j*theta)*conj(dipole)
print('check stationary value of C_theta: %3.4g + %3.4g i vs %3.4g + %5.4g i'
%(real(sTheta_corr[-1]), imag(sTheta_corr[-1]), \
real(dipole_theta**2), imag(dipole_theta**2)) )
plot( t, real(sTheta_corr), 'b--', label = r'$\mathsf{Re\ }C_\theta$' )
plot( t, imag(sTheta_corr), 'r--', label = r'$\mathsf{Im\ } C_\theta$' )
t_max = 12./gamma_e
xlim(0, t_max)
plot( [0, t_max], [real(dipole**2), real(dipole**2)], 'g:' )
plot( [0, t_max], [imag(dipole**2), imag(dipole**2)], 'g:' )
plot( [0, t_max], [real(dipole_theta**2), real(dipole_theta**2)], 'g:' )
plot( [0, t_max], [imag(dipole_theta**2), imag(dipole_theta**2)], 'g:' )
xlabel(r'$\mathsf{time\ } \gamma t$', size = mysize)
ylabel(r'$\mathsf{correlation\ } Q_\sigma( t )$', size = mysize)
legend(fontsize = mysize, loc = 'upper right')
# subtract asymptotic value and take Fourier transform
sqcorr -= sqcorr[-1]
spec = 2*real(dt*fft(sqcorr)) # not obvious that this is the right rule
# since the 'squeezing spectrum' can in general be complex
#
spec = fftshift(spec)
omega = fftshift(2*pi*fftfreq(N_t, d = dt))
figure('squeezing', (xsize, ysize), tight_layout = True)
plot(omega/gamma_e, spec, 'r-', label = r'$\sigma\sigma$')
# repeat for squeezing correlation
#
sTheta_corr -= sTheta_corr[-1]
spec = 2*real(dt*fft(sTheta_corr)) # standard rule
# because \sigma_\theta is hermitean
#
spec = fftshift(spec)
plot(omega/gamma_e, spec, 'r--', label = r'$\sigma_\theta\sigma_\theta$')
om_max = max(2.5*sqrt(abs(Rabi_f)**2 + (Laser_f - Atom_f)**2), 3.*gamma_e)
xlim(-om_max, om_max)
xlabel(r'$\mathsf{frequency\ } (\omega - \omega_L)/\gamma$', size = mysize)
ylabel(r'$\mathsf{squeezing\ } S_\sigma( \omega )$', size = mysize)
legend(fontsize = mysize)
if False:
"""
compute spectrum by Fourier transform of excited state pe(t),
gives intensity correlations
"""
# plot correlation function
figure(2, (xsize, ysize), tight_layout = True)
plot( gamma_e*t, be_rwa, 'r' )
plot( gamma_e*t, be_xrwa, 'b' )
plot( gamma_e*t, be_g2/pe, 'k', lw = 1.5 )
t_max = 5./gamma_e
xlim(0, t_max)
ylim(0, 1.05*max(be_rwa))
plot( [0, t_max], [pe, pe], ':', c = 'gray' )
xlabel(r'$\mathsf{time\ delay\ } \gamma_e \tau$', size = mysize)
ylabel(r'$\mathsf{correlation\ } C_I(\tau)$', size = mysize)
IIcorr = be_rwa - be_rwa[-1] # subtract final value
spec = 2*real(dt*fft(IIcorr))
IIcorr = be_xrwa - be_xrwa[-1]
xspec = 2*real(dt*fft(IIcorr))
# plot spectrum
figure(1, (xsize, ysize), tight_layout = True)
spec = fftshift(spec)
xspec = fftshift(xspec)
omega = fftshift(2*pi*fftfreq(N_t, d = dt))
plot(omega/gamma_e, spec, 'r-')
plot(omega/gamma_e, xspec, 'b-')
om_max = max(6*abs(Rabi_f), 8*gamma_e)
xlim(-om_max, om_max)
xlabel(r'$\mathsf{frequency\ } (\omega - \omega_L)/\gamma$', size = mysize)
ylabel(r'$\mathsf{spectrum\ } S_I( \omega )$', size = mysize)
show(block = False)


Squeezing correlations (left) and spectra (right) for a
two-level atom. Parameters as in the script.