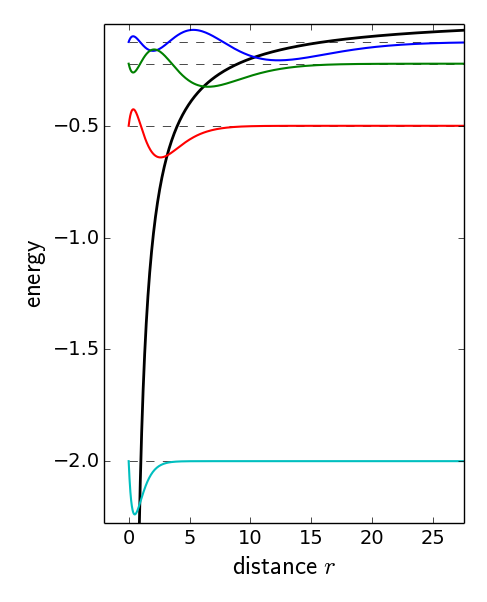
Hydrogen-like wave functions in the Coulomb potential of the Helium nucleus.
#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
2019 Nov 15, C. Henkel
Play with Hartree-Fock theory for the Helium ground state.
"""
from pylab import *
from scipy.integrate import odeint, quad, trapz
from scipy.sparse import diags, coo_matrix, csc_matrix
from scipy.sparse.construct import eye
# sparse eigenvalue solver:
from scipy.sparse.linalg import eigs, eigsh, spsolve
# adapt a few parameters for size and font size of figures
# other global parameters are set in the configuration file
# matplotlibrc that is to be placed in the directory
# ~/.matplotlib/
#
tsize = 18
xsize = 6.5
ysize = xsize*0.5*(sqrt(5)-1)
plt.rcParams['figure.figsize'] = (xsize, ysize) # 'golden ratio' = good aesthetics
plt.rcParams['figure.autolayout'] = True
plt.rcParams['font.size'] = tsize-2
plt.rcParams['axes.labelsize'] = tsize
plt.rcParams['xtick.labelsize'] = tsize-4
plt.rcParams['ytick.labelsize'] = tsize-4
def SchroedOperator(y, potl, h2 = 0.5, BC = ('D', 'D'), Q_symmetric = True):
"""
Set up Schroedinger operator on grid y (possibly non-equidistant)
using the potential potl, returning two matrices
Schroed, M = SchroedOperator(y, potl)
M is the "metric" in case of a non-equidistant grid, that
appears in the generalised eigenvalue problem
Schroed.u = lambda M.u
The norm u^T.M.u = trapz(u**2, dx = dy).
The grid y contains the end points.
For the moment, only Dirichlet 'D' BCs are implemented.
Potential potl can be a function or a list (same size as y).
Parameter h2 = hbar**2/2m.
Boundary condition BC at (left, right) end points.
"""
# boundary conditions, D or N
if size(shape(y)) > 1: # then y is a matrix, not a list
print('... I flattened y, no guarantee!')
y = flatten(y)
nb_y = size(y)
dy = diff(y)
dyPlus = dy[:-1]
dyMinus = dy[1:]
dySum = dyPlus + dyMinus
# define (band)diagonals of Schroedinger matrix
# h2 = hbar^2/(2m)
# potential from function or list
try:
V = potl(y[1:-1]) # only inner points are needed
except TypeError:
if not(size(y) == size(potl)):
print('Danger: list for potential not the same size, interpolating.')
# guess that V is given on equidistant grid with same endpoints as y
x_guess = linspace(min(y), max(y), size(potl))
V = interp(y[1:-1], x_guess, potl)
else:
V = potl[1:-1]
if not(Q_symmetric):
diag_0 = - 2*h2*(-1./(dyPlus*dyMinus)) + V
# lower diagonal
diag = - 2*h2/(dySum*dyMinus)
diag_l = diag[:-1]
# upper diagonal
diag = - 2*h2/(dySum*dyPlus)
diag_u = diag[1:]
# need some adjustment here if BC = N is taken, not yet implemented
#
Schroed = diags([diag_l, diag_0, diag_u], [-1, 0, 1], shape = (nb_y-2, nb_y-2))
M = diags(1., 0, shape = (nb_y-2, nb_y-2))
Schroed = csc_matrix(Schroed)
else:
# one gets a symmetric matrix by factoring out the derivative 1/dyS
# this yields a positive matrix M for the generalized eigenvalue problem
# S u = lambda M u
# the eigenvectors are normalized with respect to this quadratic form
# so that u^T M u = 1
# we move a factor 1/2 around, too so that M is close to a standard metric
# this norm (after extension of the state to include the end points) is
# equivalent to norm = sqrt(trapz(state[:,k]**2, dx = dy))
#
diag_0 = - h2*(-dySum/(dyPlus*dyMinus)) + 0.5*dySum*V
# lower diagonal
diag = - h2/(dyMinus)
diag_l = diag[:-1]
# upper diagonal
diag = - h2/(dyPlus)
diag_u = diag[1:]
#
Schroed = diags([diag_l, diag_0, diag_u], [-1, 0, 1], shape = (nb_y-2, nb_y-2))
M = diags(0.5*dySum, 0)
Schroed = csc_matrix(Schroed)
return Schroed, M
def solveSchroed(y, potl, h2 = 0.5, nb_k = 5, E_target = 0., BC = ('D', 'D')):
"""
Solve Schroedinger equation on grid y (possibly non-equidistant)
using the potential potl, returning real-valued results:
levels, states = solveSchroed(y, potl)
Returns energy levels (array of size nb_k)
and L2-normalised states (array of shape (size(y), nb_k))
The grid y contains the end points, for the moment, only Dirichlet
BCs are implemented.
Hence states[0,k] = 0 = states[-1,k] for all k = 0 ... nb_k - 1.
Potential potl can be a function or a list (same size as y).
Parameter h2 = hbar**2/2m.
Parameter nb_k = number of eigenvalues.
Parameter E_target = search around this energy.
Boundary condition BC at (left, right) end points.
"""
if size(shape(y)) > 1: # then y is a matrix, not a list
print('... I flattened y, no guarantee!')
y = flatten(y)
nb_y = size(y)
dy = diff(y)
dyPlus = dy[:-1]
dyMinus = dy[1:]
dySum = dyPlus + dyMinus
Q_symmetric = True
Schroed, M = SchroedOperator(y, potl = potl, h2 = h2, BC = BC,
Q_symmetric = Q_symmetric)
if not(Q_symmetric):
level, state = eigs(Schroed, k = nb_k, M = M, sigma = E_target, which = 'LM')
# discard imaginary values, are hopefully negligible
level = real(level)
state = real(state)
else:
level, state = eigsh(Schroed, k = nb_k, M = M, sigma = E_target, which = 'LM')
# this should return real energy levels, hopefully imaginary part of
# wave functions is negligible
state = real(state)
#
# insert boundary values and normalize
# extend first the array along both ends of the grid
state = pad(state, ((1,1), (0,0)), 'constant')
#
# extend symmetric difference list by linear extrapolation
dyS0 = dySum[0] + (y[0] - y[1])*(dySum[1]-dySum[0])/(y[2] - y[1])
dySum = insert(dySum, 0, dyS0)
# same for other end point of difference list
dyS1 = dySum[-1]+(y[-1]-y[-2])*(dySum[-1]-dySum[-2])/(y[-2]-y[-3])
dySum = append(dySum, dyS1)
#
for k, E in enumerate(level):
# pad values at end points, according to BC
for ix, bc in enumerate(BC):
if bc == 'D':
bc_value = 0. # zero at end point
elif bc == 'N':
bc_value = state[1 - 3*ix, k] # same value as adjacent inner point
# left (ix = 0): index 1, right (ix = 1): index -2
else:
print('... wrong BC, assuming D.')
bc_value = 0.
state[-ix, k] = bc_value # works for indices (left) 0 and (right) -1
# normalize the state
norm_k = trapz(state[:,k]**2, dx = dy)
state[:,k] /= sqrt(norm_k)
#
return level, state
if True:
# set up parameters for potential: Coulomb potential in the Helium atom
fig_title = 'Helium Coulomb problem'
x_max = 45. # outer end point (choose large compared to radial size)
x_min = 0.0 # inner end point (one error message from division by zero)
Nb_x = 358 # number of points on the grid
E_mean = -2. # search for eigenvalues around this number
# = single-particle ground state energy, exact result
nb_E = 5 # number of levels to find
# the potential in the Schroedinger equation can be given as a function
# or as a list of values (on the positions of the spatial grid y).
# Here, the construction works with a function. If a list is generated,
# remove the function definition.
def potl(x):
# define potential for radial Schroedinger equation
# ell = angular momentum quantum number
# Ze2 = nuclear charge
ell = 0
Ze2 = 2.
V = 0.5*ell*(ell+1)/x**2 - Ze2/x
# to do: add the electron-electron energy here
return V
# y = linspace(x_min, x_max, Nb_x)
# non-equidistant grid, much better precision in energy levels
y = linspace(sqrt(x_min), sqrt(x_max), Nb_x)**2
# use routine solveSchroed to solve
# Schroedinger equation numerically. Returns energy levels
# and L2-normalised states.
#
levels, states = solveSchroed(y, potl, nb_k = nb_E, E_target = E_mean)
if True:
# plot the wave functions in the 'usual representation'
# find suitable scale factor to plot the wave functions
# this is adapted to a plot of the wave functions (not the density)
#
Q_doublet = False
Q_listPot = False
scale_psi = 1.
try:
dE = min(diff(levels))
except ValueError: # happens when output has only one state
dE = 0.5*abs(max(levels))
if Q_doublet:
# take larger value when tunnelling degeneracy occurs
diffEother = delete(diff(levels), find(diff(levels) == dE))
dE = min(diffEother)
psi_max = 0.
for psi in states:
psi_max = max(psi_max, max(abs(psi)))
scale_psi = 0.45*dE/psi_max
figure(fig_title, (xsize, ysize))
if Q_listPot:
plot( y, potl, 'k', lw = 2 )
else:
plot( y, potl(y), 'k', lw = 2 )
for k in range(shape(levels)[0]-1, -1, -1):
Ek = levels[k]
plot( [min(y), max(y)], [Ek, Ek], 'k--', lw = 0.5 )
plot( y, Ek + scale_psi*states[:,k], lw = 1.5, label = r'$E_{%i} = %3.4g$' %(k, Ek))
xlabel(r'$\mathsf{position\ } x$')
ylabel(r'$\mathsf{energy\ }$')
ylim(min(levels) - dE, max(levels) + 3*dE)
# legend()
if True:
# check normalisation of eigenfunctions (L2 norm)
# here, the formulation is such that states[:,k] = psi_k(r) = r * R_k(r)
# The radial normalisation integral is therefore
# int_0^infty dr * r**2 * R(r)**2
# = int_0^infty dr * psi(r)**2
# On the non-equidistant grid y, this can be computed with the
# trapeze rule 'trapz(f, y)'
for k in range(nb_E):
# loop over levels
norm_k = trapz(states[:,k]**2, y) # the second argument gives the spatial grid
print('level %i: E_k = %3.4g' %(k, levels[k]))
print(' norm = %3.4g' %(norm_k))
# to do:
# -- compare with the exact results for the hydrogen-like wave functions
# (see photo from the Bethe & Salpeter book on the web site)
# -- generate with the ground state wave function psi_1(r) (k = ?) the
# electron-electron potential W(r) = a list on the spatial grid y.
# -- make a plot of the electron charge density, of the potential W and of
# the total potential (Coulomb pot of the nucleus plus W).
# -- include in the plot the analytical evaluation of the potential W
# with the hydrogen-like wave function (see Problem no 4.1(2)).
# -- use the potential W to 'update' the Schroedinger equation and re-compute
# the ground state wave function
# -- give the value for the Hartree-Fock energy eigenvalue epsilon_1
# -- make a plot to compare the two wave functions.
# -- compute the integrals that are needed for the Hartree-Fock ground state energy.
# -- compare to the tabulated data from the Bethe-Salpeter book.
show(block=False)

Hydrogen-like wave functions in the Coulomb potential of the
Helium nucleus.